Bonito como un caracol

4/ Seotiembre / 2018

BONITO COMO UN CARACOL

(Sección áurea y regla de tercios)

Objetivo: Reconocer y emplear en la generación de fotografías, los conceptos de sección áurea y regla de tercios.
 Vinculación semántica:

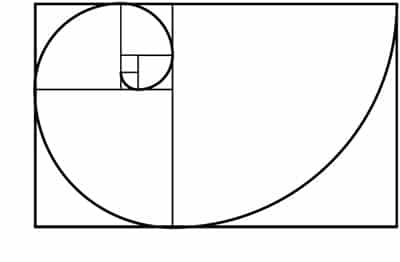
Hace muchos años la belleza estaba contemplada en algo llamado "sección áurea" el cual es un número irracional que descubrieron pensadores de la Antigüedad al advertir el vínculo existente entre dos segmentos pertenecientes a una misma recta. Dicha proporcion puede hallarse en la naturaleza (flores, hojas, etc.) y en figuras geométricas y se le otorga una condición estética: aquello cuyas formas respetan la proporción áurea es considerado bello.

Existían diferentes teorías sobre la composición. Platón decía: "Es imposible combinar bien dos cosas sin una tercera, hace falta una relación entre ellas que los ensamble, la mejor ligazón para esta relación es el todo, con esto se crea la "regla de tercios" la cual es un medio simple de aproximación a la proporción áurea, que trata la distribución del espacio dentro de la imagen que genera una mayor atracción respecto al centro de interés. Con el uso de la regla de los tercios se consigue dotar a las fotografías de una sensación de profundidad y apreciar un mayor equilibrio, guiando al espectador directamente al punto de mayor interés. con lo anterior, tendremos cuatro puntos en los que las líneas coincidirán. Estos son los llamados Puntos Fuertes o Principales de la imagen.

"La suma de las partes como todo es la más perfecta relación de proporción". Vitruvio,

acepta el mismo principio pero dice que la simetría consiste en el acuerdo de medidas entre los diversos elementos de la obra y éstos con el conjunto. Según Vitruvio, se analiza que al crear una composición, si colocamos los elementos principales del diseño en una de las líneas que dividen la sección áurea, se consigue el equilibrio entre estos elementos y el resto del diseño. Este razonamiento de sigue vigente hoy en día a la hora de componer, ya sea un edificio, una fotografía o un diseño sobre papel ya que se cree que seguir esta regla da como resultado trabajos más equilibrados y armoniosos. Se relaciona con el modelo matemático conocido como "serie de Fibonacci" la cual es una serie numérica: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. Es una serie infinita en la que la suma de dos números consecutivos siempre da como resultado el siguiente número (1+1=2; 13+21=34). La relación que existe entre cada pareja de números consecutivos (es decir, si dividimos cada número entre su anterior) se aproxima al número áureo (1,618034).